The kriging_weights algorithm solves a kriging system :
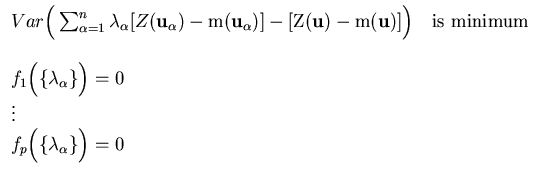
where
fi![]() {
{![]() }
}![]() = 0,
i = 1,..., p are linear constraints expressed by the Kriging Constraint Kconstraint. The solution to this system is a set of weights:
= 0,
i = 1,..., p are linear constraints expressed by the Kriging Constraint Kconstraint. The solution to this system is a set of weights:
The kriging_weights function computes the kriging weights and stores them into Vector weights in the following order:
(![]() ,...,
,...,![]() ,
,![]() ,...,
,...,![]() ).
Only the weights
).
Only the weights
![]() ,...,
,...,![]() are useful to compute the kriging estimate. The weights
are useful to compute the kriging estimate. The weights
![]() ,...,
,...,![]() are used to compute the kriging variance.
Vector weights does not need to be of the correct size n + p when passed to the function: the function automatically resizes the vector if necessary.
Two versions of the algorithm exist. Version 1 computes the kriging variance and stores it into kriging_variance, while Version 2 does not compute the kriging variance (there are cases where the kriging variance is useless, e.g. in indicator kriging).
Both version of the algorithm allow to change the linear algebra library (which defines matrices, matrix inversion routines, ...) used by kriging_weights (see 2.4).
The default linear algebra library is the TNTlibrary (slightly modified), a public domain library by Roldan Pozo, Mathematical and Computational Sciences Division,National Institute of Standards and Technology.
are used to compute the kriging variance.
Vector weights does not need to be of the correct size n + p when passed to the function: the function automatically resizes the vector if necessary.
Two versions of the algorithm exist. Version 1 computes the kriging variance and stores it into kriging_variance, while Version 2 does not compute the kriging variance (there are cases where the kriging variance is useless, e.g. in indicator kriging).
Both version of the algorithm allow to change the linear algebra library (which defines matrices, matrix inversion routines, ...) used by kriging_weights (see 2.4).
The default linear algebra library is the TNTlibrary (slightly modified), a public domain library by Roldan Pozo, Mathematical and Computational Sciences Division,National Institute of Standards and Technology.
The value returned by kriging_weights indicates if any problem were encountered:
However, each call to kriging_weights implies solving a linear system of equations, hence the cost of the resize would usually be negligible.
typedef std::vector<geo_value2d> neighborhood;
// gaussian covariance of range 4
inline double gauss_covariance(Location2d u1, Location2d u2){
double square_dist = pow(u1[0]-u2[0], 2) +
pow(u1[1]-u2.[1], 2);
return exp(-3*square_dist/16);
}
int main()
{
location2d u1(2,3);
location2d u2(4,-7);
geo_value2d Z1(u1,0.21);
geo_value2d Z2(u2,0.09);
Neighborhood neighbors;
neighbors.push_back(Z1);
neighbors.push_back(Z2);
location2d u(0,0);
std::vector<double> weights;
double kvariance;
kriging_weights(weights, kvariance,
u, &neighbors,
gauss_covariance, OK_constraint);
}