MM1 Covariance

MM1_covariance<covariance, matrix>

Full cokriging of Z₁ accounting for secondary variables Z₂,..., Z_Nv requires the inference of all covariance functions ($\bf u_{1}^{}$,$\bf u_{2}^{}$) $\longmapsto$ C_{i, j}($\bf u_{1}^{}$,$\bf u_{2}^{}$) between variables i and j. This very difficult task can be eased by considering only the colocated secondary variables. The underlying hypotheses is that the colocated value screens out the influence of further away data. In this situation, only the covariances C_{1, j} need be inferred. The MM1 approximation alleviate the modeling effort further with the following approximation:

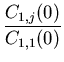C_{1, j}($$\bf u_{1}^{}$$,$$\bf u_{2}^{}$$) = $${\frac{C_{1,j}(0)}{C_{1,1}(0)}}$$C_{1, 1}($$\bf u_{1}^{}$$,$$\bf u_{2}^{}$$)

where C_{i, j}(0) = C_{i, j}($\bf u_{1}^{}$,$\bf u_{1}^{}$) = C_{i, j}($\bf u_{2}^{}$,$\bf u_{2}^{}$)

This approximation is acceptable if the support of the secondary variables is not larger than the support of the primary variable Z₁. For example, if Z₁ is rock porosity and Z₂ rock permeability, MM1 approximation is acceptable. It would not be if Z₂ were seismic amplitude, because seismic amplitude is generally defined on a much larger scale than porosity.

Where Defined

In header file <kriging.h>

Template Parameters

covariance		is a model of Covariance
matrix		is an object that represents a matrix. Expression mat(i,j) must be valid and return element (i,j) of the matrix (i and j are greater than or equal to 1), and the matrix must have a copy constructor. The elements of matrix are of type convertible to double.

Model of

Covariance Set

Type Requirements

The elements of the matrix are of type convertible to double.

Members

• MM1_covariance::MM1_covariance(const covariance& cov,
                                 const matrix& A, unsigned int size)
  
  Constructs a MM1_covariance. Covariance function cov is C_{1, 1}, and matrix A contains the covariance values C_{i, j}(0). Notice that matrix A contains numbers, not pointers to functions as in LMC. size is the size of the covariance matrix. It is equal to the number of variables N_v.

• double MM1_covariance::operator()(unsigned int i, unsigned int j,
                                    const location& u1, const location& u2)
  
  Function call operator. Returns the covariance C_{i, j}($\bf u_{1}^{}$,$\bf u_{2}^{}$) using the MM1 approximation.