MM2 Covariance

MM2_covariance<covariance_vector, matrix>

The MM1 approximation is not valid if the support of the secondary variables is larger than the support of the primary variable. In this case, the covariances C_{1, j} can be approximated as follows (MM2 hypothesis):

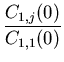C_{1, j}($$\bf u_{1}^{}$$,$$\bf u_{2}^{}$$) = $${\frac{C_{1,j}(0)}{C_{1,1}(0)}}$$C_{j, j}($$\bf u_{1}^{}$$,$$\bf u_{2}^{}$$)

This approximation is less convenient than the MM1 approximation, because it requires the inference of all covariances C_{j, j}.

Where Defined

In header file <kriging.h>

Template Parameters

covariance_vector		is an object that has member function covariance_vector[int i], that returns element i of the vector (i is greater than or equal to 0). The elements of the vector must be models of Covariance. covariance_vector must also have a copy constructor.
matrix		is an object that represents a matrix. Expression mat(i,j) must be valid and return element (i,j) of the matrix (i and j are greater than or equal to 1), and the matrix must have a copy constructor. The elements of matrix are of type convertible to double.

Model of

Covariance Set

Type Requirements

• The elements of the matrix are of type convertible to double.

• covariance_vector contains pointers to models of Covariance.

Members

• MM2_covariance::MM2_covariance(covariance_vector& cov_vect,
                                 const matrix& A, unsigned int size)
  
  Constructs a MM2_covariance. cov_vect contains pointers to the covariance functions C_{i, i}, i = 1,..., N_v.

  Matrix A contains the covariance values C_{i, j}(0). Notice that matrix A contains numbers, not pointers to functions as in LMC.

  size is the size of the covariance matrix. It is equal to the number of variables N_v.

• double MM2_covariance::operator()(unsigned int i, unsigned int j,
                                    const location& u1, const location& u2)
  
  Function call operator. Returns the covariance C_{i, j}($\bf u_{1}^{}$,$\bf u_{2}^{}$) using the MM1 approximation.